So yesterday, I passed through this post in my Facebook feeds. This was shared to one LET Review group.
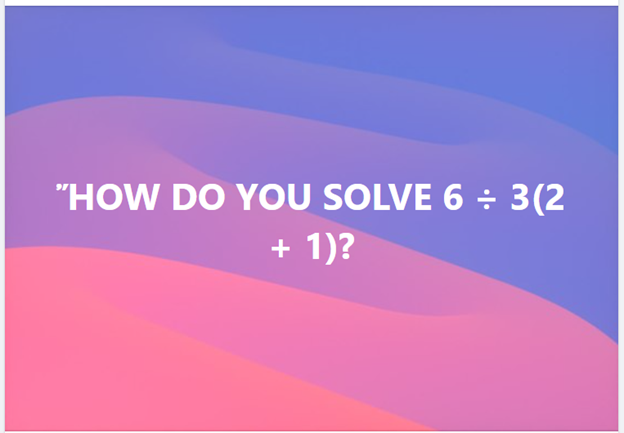
For most of you, this must be a simple problem but I was surprised by how many people got this wrong. So for today’s LET Review post and video, we will be discussing the order of operations in mathematics.
If you are new here, welcome to the LETPasser.com review YouTube channel. Wag na mahiyang mag subscribe to help out the channel. We are posting a few LET review question every week. If you are reviewing right now, please bookmark this page, subscribe to the YouTube channel and follow our Facebook group.
Let’s begin.
Let’s go back to the equation: 6 ÷ 3 ( 2+1 )
Before we proceed with the answer to the problem, how about you solve this first to check if you know the answer. If you are ready with the answer, you can proceed below.
—————————–Don’t Cross before you have an answer—————————
The answer is 6. The equation goes as follows:
6 ÷3 ( 2+1 )
= 6 ÷ 3 (3)
= 2 (3)
= 6
Simple enough. If you answered this right, congratulations. You may move on to other review topics. If you missed this, let’s check where made a mistake.
The Rule
In math, we refer to this as the order of operations. Operations refer to adding (+), subtracting (-), dividing (÷) and multiplying (x). Aside from these, the other two operations are the use of parenthesis () and exponents (nX).
This rule in math tells us the order by which we perform these operations. For example, the rule tells us that in this equation:
2 + 3 x 4
We must multiply first before we add. In this case, the answer is 14:
2 + 3 x 4
= 2 + 12
= 14
Here is the order if all the operations are involved:
- Parenthesis – Solve all equations inside the parenthesis first.
- Exponents – apply all exponents first
- Multiplication & Division – you multiply or divide first depending on which one comes first (left to right)
- Addition & Substraction – You add or subtract first depending on which one comes first (left to right)
The Mnemonic
To make it easier to remember, teachers use the mnemonic PEMDAS. This is where the confusion starts for most test takers. Because M comes before D in the abbreviation, many think that multiplication always comes before division. This is the first mistake.
If you go back to the order of operations rule, multiplication and division are in the same level. You do the operations from left to right for division and multiplication. The same applies for addition and subtraction. Let’s take this example:
5 + 2 ÷ 2 + 12 ÷ 4 x 2 – 5
First you do the first division operation: 5 + 2 ÷ 2 + 12 ÷ 4 x 2 – 5
= 5 + 1 + 12 ÷ 4 x 2 – 5
Next, you do the next division operation: = 5 + 1 + 12 ÷ 4 x 2 – 5
= 5 + 1 + 3 x 2 – 5
Only then will you do the multiplication: = 5 + 1 + 3 x 2 – 5
= 5 + 1 + 6 – 5
Now, you apply the same rule for addition and subtraction:
= 5 + 1 + 6 – 5
= 6 + 6 – 5
= 12 – 5
=7
To make this easier to remember, use this mnemonic: P E M&D A&S
Now, let’s practice. Solve the following:
A) 9 + 2 – 3 x 2 + ( 9 – 7 x 4)
B) 8 – 6 ÷ 3 + 2 x 1 + 4
C) 9 ÷ 3 x 2 x 3 + 4
Leave your answers in the comments.